Demonstrating That Projectile Motion Is Parabolic

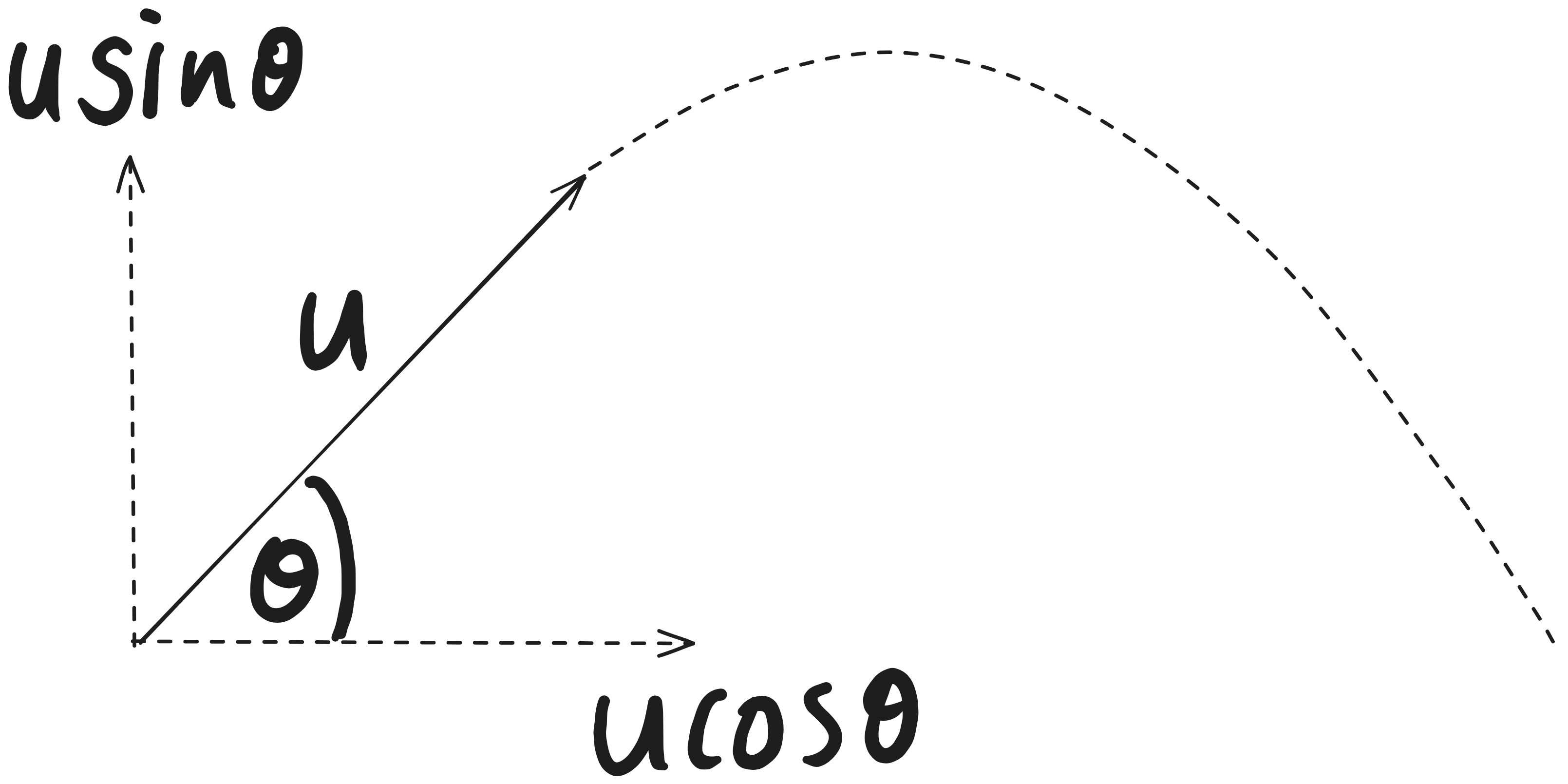
Recall that the following do not change for projectile motion, given that the angle of projection($\theta$) is relative to the horizontal:

• $u_x=u\cos{\theta}$
• $u_y=u\sin{\theta}$
• $a_x=0$
• $a_y=-g$
  View Original

  

Projectile motion can be represented by a parabola of the form: $$y=ax^2+bx+c$$

We can use the formula for displacement($s$) written in terms of initial velocity($u$), acceleration($a$) and time($t$): $$s=ut+\frac12at^2$$

Applying it to the x direction: $$s_x=u_xt+\frac12a_xt^2$$

We know that $u_x=u\cos{\theta}$ and $a_x=0$: $$s_x=ut\cos{\theta}$$

Note that we do not write $u\cos{\theta t}$ because it implies that the time($t$) is part of the angle being governed by cosine. It is more appropriate to write $(u\cos{\theta})t$ and then rewrite this as $ut\cos{\theta}$

Applying it to the y direction: $$s_y=u_yt+\frac12a_yt^2$$

We know that $u_y=u\sin{\theta}$ and $a_y=-g$: $$s_y=ut\sin{\theta}-\frac12gt^2$$

We can let $s_x$ be $x$ and $s_y$ be $y$ to make visualizing them as parametric equations easier: $$x=ut\cos{\theta}$$ $$y=ut\sin{\theta}-\frac12gt^2$$

Because $u$ and $\theta$ are constants for a given projectile, we essentially have $x$ and $y$ written in terms of $t$. This makes them parametric equations with the parameter being time, $t$.

Transposing for $t$ in equation 1: $$t=\frac{x}{u\cos{\theta}}$$

Substituting this into the second equation: $$\begin{equation}\begin{aligned} y&=u(\frac{x}{u\cos{\theta}})\sin{\theta}-\frac12g(\frac{x}{u\cos{\theta}})^2\\ y&=x\tan{\theta}-\frac12g(\frac{x^2}{u^2\cos^2{\theta}})\\ y&=x\color{red}\tan{\theta}\color{normal}\color{royalblue}-\frac{g\sec^2{\theta}}{2u^2}\color{normal}x^2\\ y&=\color{royalblue}a\color{normal}x^2+\color{red}b\color{normal}x+c\\ \end{aligned}\end{equation}$$

What are the coefficients of $x^2$ and $x$ written in terms of $u$, $\theta$ and $g$? What is the value of the constant $c$?